Definición y Nomenclatura de Cuadriláteros.
Un cuadrilátero es un polígono de cuatro lados y por lo tanto cuatro vértices. Al igual que en los triángulos sus ángulos y vértices se nombran con letra mayúscula y en el sentido contrario al de las agujas de un reloj. Siguiendo este mismo sentido, los lados se nombran con la misma letra , en minúscula, del vértice que le precede.
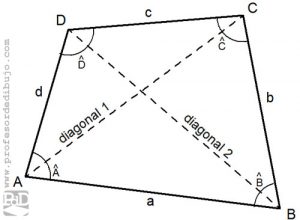
La diagonal es el segmento que une dos vértices no consecutivos de un polígono. En el caso de los cuadriláteros tenemos dos: AC y BD. cada diagonal de un cuadrilátero divide a este en dos triángulos.
La suma de los ángulos interiores de un cuadrilátero es 360º.
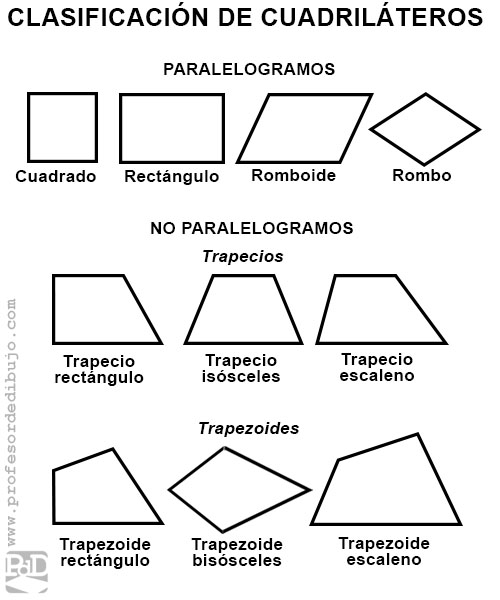
Clasificación de los cuadriláteros.
Atendiendo al paralelismo de sus lados se pueden clasificar en dos grupos principales:
- Paralelogramos: son aquellos cuadriláteros que tienen todos los lados opuestos paralelos dos a dos. Como características generales de los paralelogramos podemos enumerar las siguientes:Los lados opuestos siempre son iguales. Miden lo mismo.
También son iguales sus ángulos opuestos.
Dos ángulos consecutivos son complementarios.
Las diagonales se bisecan, es decir, se cortan en sus puntos medios y ambos quedan divididos en sus mitades.
Cada diagonal divide al paralelogramo en dos triángulos iguales.- Cuadrado: es el cuadrilátero regular. Por lo tanto todos sus lados y ángulos son iguales. Dichos ángulos son rectos (90º). Sus dos diagonales son iguales y se cortan formando también ángulos rectos.
- Rectángulo: son cuadriláteros que tienen los lados opuestos iguales dos a dos y ángulos rectos (90º). Sus diagonales también son iguales, pero al cortarse no forman ángulo de 90º.
- Rombo: es un cuadrilátero que tiene los cuatro lados iguales, pero sus ángulos (distintos a 90º) sólo son iguales al opuesto. Sus diagonales tienen medida distinta, pero si forman ángulo recto.
- Romboide: son cuadriláteros que tienen lados y ángulos que solamente son iguales a su opuesto. Sus diagonales no miden lo mismo y se cortan formando ángulos distintos a 90º.
Otra característica particular es que en el cuadrado y el rombo, las diagonales son las bisectrices de los ángulos de la figura. - No paralelogramos: son todos aquellos cuadriláteros que no cumplen la condición de los paralelogramos.
Dentro de esta categoría podemos distinguir dos grandes grupos.- Trapecios: Son cuadriláteros que sólo tienen dos lados opuestos paralelos.
A su vez se pueden clasificar en tres tipos.- Trapecios rectángulos: tienen dos ángulos rectos.
- Trapecios isósceles: sus lados no paralelos miden lo mismo y sus ángulos son iguales dos a dos.
- Trapecios escalenos: tienen todos los ángulos y lados desiguales.
- Trapezoides: Son cuadriláteros que no tienen ningún lado paralelo a otro.
A su vez se pueden clasificar en tres tipos.- Trapezoides rectángulos: tienen un ángulo recto.
- Trapezoides bisósceles: tienen dos pares de lados iguales y son consecutivos. También tiene dos ángulos opuestos iguales. Sus diagonales forman ángulo recto.
- Trapezoides escalenos: tienen todos los ángulos y lados desiguales.
- Trapecios: Son cuadriláteros que sólo tienen dos lados opuestos paralelos.
Otras propiedades interesantes sobre cuadriláteros:
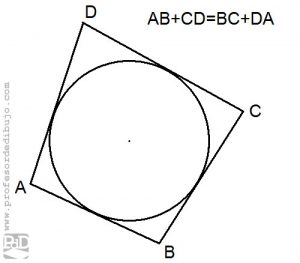
- Cuando la suma de los lados opuestos de un cuadrilátero es de igual magnitud, es decir coincide, este tiene una circunferencia inscrita en su interior, circunscrita. Esto significa que existe una circunferencia interior tangente a los cuatro lados de la figura.
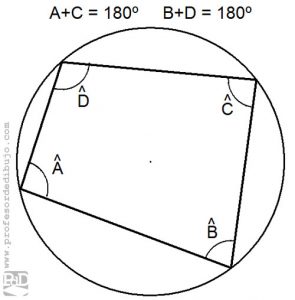
- Si los ángulos opuestos de un cuadrilátero son suplementarios existe una circunferencia que lo circunscribe. Es decir, el cuadrilátero es inscribible en una circunferencia que pasa por sus cuatro vértices.